Section A.3 Writing Mathematics, Part I
Mathematics is more than just performing calculations. It is about ideas: how concepts and calculations come together to tell a story.
Effective writing tells the story well and conveys meaning to the audience.
Remark A.3.1. Some Tips for Effective Math Writing.
- First of all, the math is correct.
- The solution is well-organized; logical structure is easy to follow.
- Steps are justified/explained as appropriate to the audience.
- Solution is written in complete sentences.
- Words (therefore, because, for all) are used instead of symbols (
- Equal signs and right-arrows are not just chained together.
Check Writing Math Well by Francis Su for some nice handouts.
When your TA or instructor reads your work what exactly are they looking for? How do they assign a grade to your solution or proof?
Consider the following statement, and suppose that the proof inside the solution link was submitted by a student.
Example A.3.2. Prove this identity.
If \(n\) is a natural number, then
Proof \(n = 1: 1 = 1\) OK.
\(n = k: 1 + 3 + 5 + \cdots + (2k-1) = k^2\)
The hypothesis is, \(n = k + 1: 1 + 3 + 5 + \cdots + (2(k+1) - 1) = (k+1)^2\text{.}\)
done.
Remark A.3.3. Rubric for Writing.
Every solution or proof you submit in the assignments or term test will be assigned two grades: one for the mathematics and one for the writing. This rubric will be used to assign the writing grade.
- 2 points: Explanations are well-written and appropriate to the target audience, MAT202 students. Guiding text and connecting words make clear the structure of the overall argument. Mathematical symbols are used correctly and convey ideas well. There are no typos or proofreading errors.
- 1 point: The solution or proof is somewhat understandable, and the main argument can still be followed. But there are minor errors in organization or the writing, or some justifications may be unclear.
- 0 points: Problems with the writing interfere with audience understanding/most of the solution not written in complete sentences or using words.
Checkpoint A.3.4. Grade and Reflect.
What grade (out of 2 points) would you give the proof in Example A.3.2 using the rubric in Remark A.3.3? Then think about the following guide questions:
- Why did you assign it the grade that you did?
- Were there any errors in the mathematics of the proof?
- What feedback would you give the student?
Now consider the following problem:
Example A.3.5. Counting Problem.
How many arrangements of the word NEWFOUNDLAND have the three N's together but the two D's apart?
In each checkpoint below there is a solution to Example A.3.5. To each one assign a grade out of 2 points based on Remark A.3.3.
Checkpoint A.3.6.
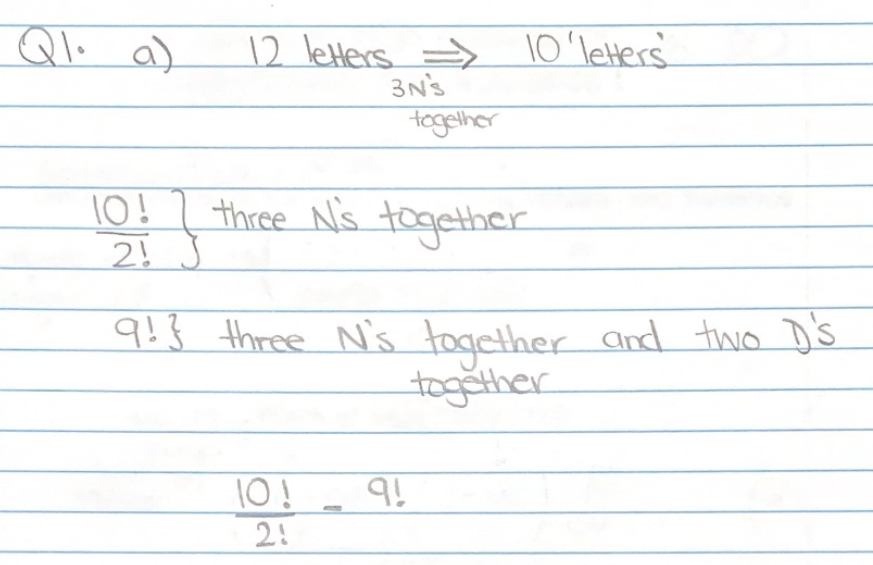
Checkpoint A.3.7.
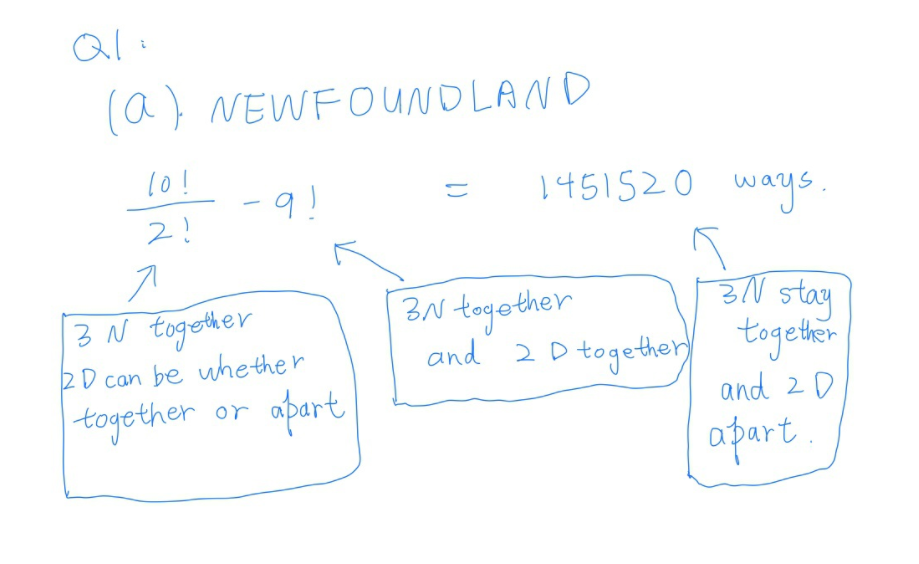
Checkpoint A.3.8.

Checkpoint A.3.9.

Checkpoint A.3.10.

Checkpoint A.3.11.
